11452. Длинный
путь
Задан ориентированный граф G с n вершинами и m ребрами. Вершины пронумерованы от 1 до n. Для каждого i (1 ≤ i ≤ m) задано
направленное ребро из вершины xi в
вершину уi.
Граф G не содержит направленных
циклов.
Найдите длину самого длинного
направленного пути в G. Под длиной пути понимается количество рёбер в этом
пути.
Вход. Первая строка содержит два целых
числа: количество вершин n (2 ≤ n ≤ 105) и
количество ребер m (1 ≤
m ≤ 105) графа. Каждая из следующих m строк
содержит два целых числа xi, уi (1 ≤ xi,
уi ≤ n), описывающих ориентированное ребро из
вершины xi в вершину уi.
Выход. Выведите длину самого длинного
направленного пути в графе G.
|
Пример
входа 1 |
Пример
выхода 1 |
|
4 5 1 2 1 3 3 2 2 4 3 4 |
3 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
6 3 2 3 4 5 5 6 |
2 |
РЕШЕНИЕ
графы – топологическая
сортировка
Анализ алгоритма
Найдем топологическую сортировку графа. Обозначим через dp[u]
максимальное количество городов, которое можно посетить по пути, начиная из
вершины u.
Рассмотрим вершины в порядке топологической сортировки. Пусть u –
текущая вершина. Обозначим через v1, v2,
…, vk вершины, в которые
ведут ребра из u. Тогда обновим значение:
dp[u] = max(dp[vi]
+ 1), 1 ≤ i ≤ k
Изначально
установим dp[u] = 0 (1 ≤ u ≤ n).
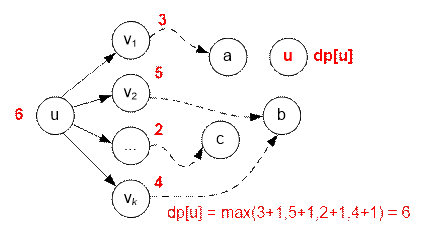
После обработки всех вершин находим наибольшее значение в массиве dp. Оно равно длине максимального пути в графе.
Пример
Слева приведен граф из первого примера. Справа – из второго. Самые длинные пути выделены.
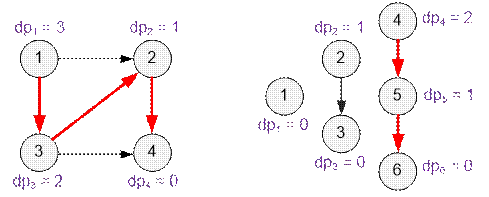
В первом примере самый длинный путь равен dp1 = 3.
Во втором примере самый длинный путь равен dp4 = 2.
Реализация алгоритма
Объявим список смежности графа g.
vector<vector<int> > g;
Функция dfs выполняет поиск в глубину, начиная с вершины v.
Сортируем вершины графа топологически и записываем их в массив top.
void dfs(int v)
{
used[v] = 1;
for (int to : g[v])
if (used[to] == 0) dfs(to);
top.push_back(v);
}
Основная часть программы. Читаем входные данные. Строим список смежности
ориентированного графа.
scanf("%d %d", &n, &m);
g.resize(n
+ 1);
while (m--)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
}
Запускаем поиск в глубину на несвязном графе.
used.resize(n
+ 1);
for (i = 1; i <= n; i++)
if (used[i] == 0) dfs(i);
Перебираем вершины графа в порядке, обратном их топологической сортировке,
то есть перебираем вершины массива top слева направо.
dp.resize(n
+ 1);
for (int u : top)
{
Путь из вершины u в саму себя имеет длину
0 (инициализация).
dp[u] = 0;
Перебираем вершины v, смежные с u. Рассматриваем
ребро (u, v).
for (int v : g[u])
Для всех таких вершин v ищем максимум среди значений dp[v]
+ 1.
dp[u] = max(dp[u], dp[v] + 1);
}
Находим и выводим наибольший элемент в массиве dp. Он соответствует длине
самого длинного пути в графе.
res = *max_element(dp.begin(), dp.end());
printf("%d\n", res);